Arbeitsauftrag 3

Die Neuner-Probe

Auf dieser Sonderbriefmarke zum 500. Geburtstag von Ries fällt das Kreuz mit dem vier Zahlen 3, 6, 3 und 6 ins Auge. Es erinnert an das Verfahren zur Neuner-Rechenprobe, das von Adam Ries vorgeschlagen wurde. Erinnerst du dich: Den Rest einer Zahl bei der Division durch 9 erhält man, indem man (wenn nötig mehrmals hintereinander) die Quersumme der Ausgangszahl bildet.

Z.B.:
321 lässt bei der Division durch 9 den Rest 6, denn die Quersumme von 321 ist 3+2+1=6 und
7869 ergibt bei Division durch 9 den Rest 3, denn 7869 hat die Quersumme 7+8+6+9=30
und 30 wiederum hat die Quersumme 3+0=3.

Die Rechenproben-Idee von Ries wollen wir an einer Aufgabe aus einem seiner Manuskript anschauen. Es ging dabei um das Überprüfen der Rechnung
7869 + 8796 = 16665
mit der Neunerprobe.
Wenn die Rechnung richtig ist, dann muss die Summe der beiden Neuner-Reste auf der linken Gleichungsseite gleich dem Neuner-Rest der rechten Seite sein.

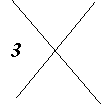Prüfen wir es nach: 7869 hat die Quersumme ....... . Diese Zahl ist schon in das linke Feld des Kreuzes eingetragen. 8796 hat die Quersumme ........ . Trage diese Zahl in das rechte Kreuzfeld ein. Die Summe dieser beiden Quersummenzahlen ist ....... . Das ist die Zahl, die in das untere Kreuzfeld kommt. Das zu prüfende Ergebnis 16665 hat die Quersumme ......... . Schreibe diese Zahl in das obere Kreuzfeld.

Stimmen oberes und unteres Kreuzfeld überein? Dann hat unsere Neuner-Probe keinen Rechenfehler aufgedeckt!