1. Lebensdaten
| 1883 |
Am 6. Januar wurde HANS BRANDES als viertes Kind des
Dorflehrers und Kantors FERDINAND BRANDES und seiner Ehefrau SOPHIE BRANDES, geb. LÖHR, in Nordassel
im Herzogtum Braunschweig geboren. Er wurde in der evang. luth. Kirche getauft. |
| 1895-1902 | Besuch des Königlichen Andreas-Realgymnasiums im preußischen Hildesheim. In den letzten Schuljahren waren GUSTAV ADOLF KALCKHOFF (~1835-1909) und FRIDO OESTERN seine Mathematik- und Physiklehrer. Er verließ das Gymnasium mit der Note sehr gut in Mathematik, um sich dem Studium der Mathematik zu widmen. |
| 1902-1904 |
Studium der Mathematik an der Universität Göttingen. Er hörte bei DAVID HILBERT (1862-1943) insbesondere den damals üblichen zweisemestrigen Grundkurs in Differential- und Integralrechnung, aber auch Theorie der Differentialgleichungen und Theorie der partiellen Differentialgleichungen. Bei HERBERT MINKOWSKI (1864-1909) besuchte er die Grundvorlesungen Algebra und Mechanik I und bei ERNST ZERMELO (1871-1953) über Determinanten. Schließlich belegte er bei FRIEDRICH SCHILLING (1868-1950) Analytische Geometrie, Analytische Theorie der krummen Linien und Flächen sowie Darstellende und projektive Geometrie und Graphische Statik. |
| 1904-1906 |
Für fünf Semester setzte BRANDES seine Studien an der Universität Halle fort. Hier wurde er stark von ALBERT WANGERIN (1844-1933) geprägt, bei dem er die Vorlesungen Elliptische Funktionen, Elliptische Funktionen II, Potentialtheorie sowie Sphärische Trigonometrie besuchte. Bei FELIX BERNSTEIN (1878-1956) hörte er Versicherungsmathematik und über Geschichte der Mathematik. Bei AUGUST GUTZMER (1860-1924) besuchte er die Funktionentheorie. Sowohl in Göttingen als auch in Halle widmete BRANDES sich intensiv dem Studium der Physik und Philosophie. |
| 1907 |
Am 5. und 6. Juli legte BRANDES in Halle vor der Königlich Wissenschaftlichen Prüfungskommission für die Provinz Sachsen sein Staatsexamen für das Lehramt an höheren Schulen ab; eine Ergänzungsprüfung fand am 13. September statt. Damit hatte er seine Lehrbefähigung in Mathematik und Physik nachgewiesen. |
| 1907 |
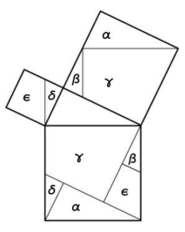
Etwa im August reicht BRANDES seine auf Anregung von BERNSTEIN entstandene Dissertationsschrift Über die axiomatische Einfachheit mit besonderer Berücksichtigung der auf Addition beruhenden Zerlegungsbeweise des Pythagoräischen Lehrsatzes bei der Philosophischen Fakultät der Universität Halle ein. Nach deren positiven Begutachtung durch GUTZMER und Annahme durch die Fakultät finded das Rigorosum am 23. November statt. Die Brandes im Frühjahr 1908 überreichte Promotionsurkunde trägt das Datum vom 4. Mai 1908. |
| 1907/08 |
BRANDES ist vom 1. Oktober 1907 bis 30. September 1908 als Seminarkandidat an dem Herzoglichen Wilhelm-Gymnasium zu Braunschweig beschäftigt. |
| 1908/09 |
Als Einjährig-Freiwilliger erfüllt BRANDES in Berlin seine militärische Dienstpflicht bei der Abteilung für drahtlose Telegraphie; er wurde zum Funkeroffizier ausgebildet. |
| 1909/10 |
Sein Probejahr absolviert BRANDES vom 1. Oktober 1909 an als wissenschaftlicher Hülfslehrer am Herzoglichen Gymnasium zu Helmstedt. Er hat alle Klassen bis zur Unterprima zu unterrichten: Mathematik, Physik, Naturkunde, Erdkunde, Rechnen und Turnen, insgesamt 22 bzw. 23 Wochenstunden! |
| 1911-1914 |
Mit Wirkung vom 1. April 1911 wird BRANDES in Braunschweig als Oberlehrer an der Städtischen Realschule (Oberrealschule in Entwicklung) angestellt. Ab Ostern 1913 ist dies die Gaußschule, Städtische Oberrealschule am Löwenwall. Er wird zunächst schwerpunktmäßig in den unteren Klassen eingesetzt, in denen er Rechnen, Geometrie, Mathematik und Naturbeschreibung zu unterrichten hat. Nach und nach wird er auch mit Unterricht in den oberen Klassen betraut. Mathematik, Physik und Linearzeichnen sind hier seine hauptsächlich gegebenen Fächer.
Mindestens seit 1912 wird BRANDES, wie auch alle seine gleichaltrigen Kollegen, jedes Jahr zu achtwöchigen militärischen Übungen eingezogen. |
| 1914-1918 |
Teilnahme am Ersten Weltkrieg als Leutnant der Reserve an der Schweren Funkerstation beim Oberkommando der IV. Armee. |
| 1919-1945 |
Nach dem Krieg kehrte BRANDES an seine alte Schule in Braunschweig zurück und hat hier schon bald nur noch die oberen Klassen in Mathematik, Physik und Linearzeichnen zu unterrichten. Mit den Unterrichtsjahren entwickelte sich BRANDES zu einem Oberstufenlehrer, dessen fachliche Kompetenz allgemein anerkannt war. Von den Schülern wird er als sehr strenger, aber gerechter Lehrer respektiert. Über viele Jahre betreute er die Sammlung für Physik und Mathematik der Schule. |
| 1931-1945 |
OTTO ZOLL (1878-1952) gibt in diesen Jahren das mehrbändige und wiederholt überarbeitete Mathematische Arbeits- und Lehrbuch für alle Arten höherer Lehranstalten heraus; hier ist unter [4] nur der 1931 erschienene erste Band zitiert. BRANDES hat an diesem Lehrwerk als Autor der Kapitel über Trigonometrie, Sphärische Trigonometrie u. a. engagiert mitgewirkt. |
| 1945-1948 | BRANDES gehört zu den wenigen Lehrern der Gaußschule, die nach dem Ende der NS-Zeit im Dezember 1945 die sofortige Lehrerlaubnis der alliierten Besatzungsbehörden erhalten. Ostern 1948 geht er in den Ruhestand. |
| 1950 | Im Vieweg Verlag Braunschweig erscheinen unter der Herausgeberschaft von BRANDES zwei überarbeitete Bände [2] des ZOLLschen Lehrwerkes. |
| 1965 | Tod am 16. Juni in Braunschweig. |